A Morphic Palindrome Grammar and its Program

Programming Aspects: 

A grammar for asymmetric palindromes

This note gives the first grammar for asymmetric palindromes as they had been introduced in previous papers.

Why are 'asymmetric' palindromes of importance?

Every body knows the famous palindromes in phonetic writing systems.

The simplest western example is the name "anna". It reads forwards and backwards the same and it has for both ways of reading the same meaning.

There are competitions about the longest palindrome, and there are even novels written as a palindrome.

But again, their meaning is invariant of the reading direction.

Therefore they are sometimes called symmetric palindromes. But in fact, all palindromes are symmetric.

Now, what is an example for an asymmetric palindrome?

I don't know a single asymmetric palindrome in a linguistic version of what ever length and elaboration.

Chinese example

 
      友朋小吃 （you meng xiaochi : a snack bar named You-Peng
 
      吃小朋友 （chi xiao pengyou  : “Eat little kids”


       http://blog.chinesehour.com/

Hence, this very small palindrome is asymmetric in its meaning, albeit its scripture is symmetric. And, again, I don't know of a single Western example of this kind of palindromes.

Now, I introduced the concept of asymmetric palindrome that are neither linguistic nor numeric or pictographic.

The simple example is the name "Annabelle". Taken as a name it isn't palindromic at all. 

Funny enough, it consists of 3 palindromes: "anna", "b", "elle". But as a composition it isn't a palindrome.

Taken as a pattern of differentiations it is a palindrome. It reads forwards and backwards as the same. 

OK, it is an asymmetric palindrome which reads the same independently of the reading direction albeit it is inscribed differently.

 "Annabelle" gets a palindromic interpretation by the asymmetric morphogram [1,2,2,1,3,4,5,5,4].

ispalindrome[1,2,2,1,3,4,5,5,4];
val it = true : bool

More at:
http://memristors.memristics.com/Morphospheres/Asymmetric%20Palindromes.html
http://the-chinese-challenge.blogspot.co.uk/2012/12/morphosperes-asymmetric-palindromes.html

Towards Grammars and Programming

Programming classical palindromes is straight forwards, easy to access and realized in all programming languages.


http://rosettacode.org/wiki/Palindrome_detection

In general there are 2 approaches to consider:

1. The non-recursive and 

2. The recursive approach.

The non-recursive works with the construct “reverse”, the recursive works over the constructs “head” and “last” of a list.


For the morphogrammatic approach, the descriptive approach has to completed by
 the rules of
   
    a) reversion

    b) repetition and


    c) accretion.

Example



This case  got a presentation in previous papers.
http://memristors.memristics.com/Formal%20Aspects/Formal%20Aspects.html

The (retro-)recursive morphogrammatic approach has to deal additionally with the concept of trito-normal form, tnf, which is the operator to produce a canonical form by  “relabeling by ascending order”.

But more important for the morphogrammatic approach is the use of the variability of the head (first) and last function for lists.

This variability is ruled by the morphoRules of the grammar for morphic palindromes.

Recursive definition of morphic palindromes


Basis: [⌀] and [1] are morphic palindromes
Induction: If for [w] = [w1w2], [w] is a palindrome, so are

Rules

R1: [w] ⟶ w1[w]w2

R2: [w] ⟶ w2[w]w1

R3: [w] ⟶ w3[w]w3

R4: [w] ⟶ w3[w]w4.

Defs

w3 = add(|w1|,1)

w4 = add(|w3|,1)

Closure

No string is a morphic palindrome of ∑(w), unless it follows from this basis and the inductive rules R1 - R4.

With that, inductive proofs of properties of morphoGrammars are enabled.

Hence, [⌀]  ⟶ [1,1], [1,2]                   : R1, R4
          
           [1]  ⟶ [1,1,1], [2,1,2], [2,1,3] : R1, R3, R4
         

The example shows how to apply the rules on the base of the normed palindrome [1,2,3,4]:

Scala Program
The morphic palindrome rules are programmed by the Scala program MorphoGrammar.

This program is not yet producing the list of palindromes of arbitrary length but is functioning as a recursive palindrome tester for the lists defined by the morphoRules.

In a next step the production of the morphic palindromes will be implemented.

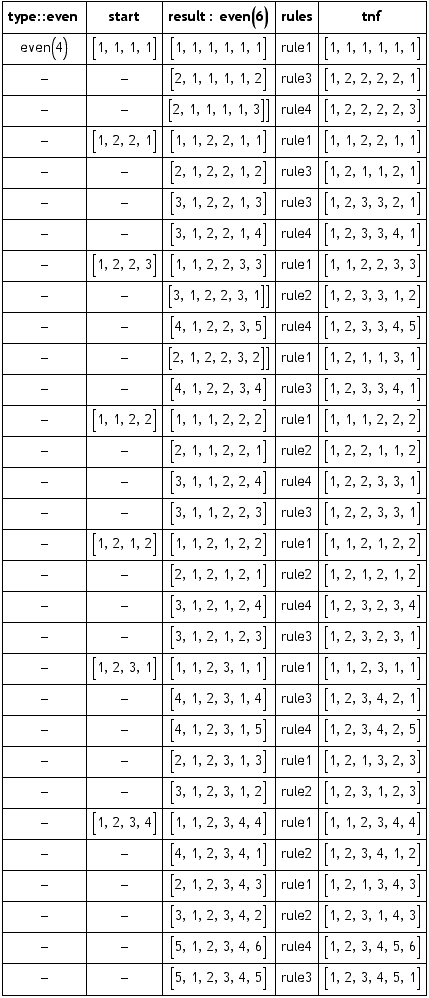
Results for odd and even palindromes are collected in the two following tables.

Remarks to the use of the tables
The following tables had been manually produced on the base of normed palindromes in trito-normal form, tnf, as it is used in the ML implementation.

The Scala program for the recursive production of palindromes, MorphoGrammar, is not yet accepting this approach. It is based purely, as it is defined, on non-canonized palindromes.

Hence, a morphogram [1,2,3] is not accepted as a palindrome by the MorphoGrammar program. Written as the list (1,2,3) it is not recognized as a morphogram that is written as [1,2,3].

scala> isPalindrome2(List(1,2,3))
res17: Boolean = false

With the list written in the form as it is produced, i.e. as the lists (2,1,3) or (3,1,2), the morphogram [1,2,3] is accepted by the MorphoGrammar as a palindrome.

scala> isPalindrome2(List(2,1,3))
res2: Boolean = true

Hence, the approach of the tables applies some kind of zigzagging between produced and normed palindromes. The start palindromes are normed, the produced palindromes are a mix of normed stars and not normed productions.

This approach is accepted by the ML implementation but not yet by the Scala program.

More at: 
http://memristics.com/Grammars and Programs/Grammars and Programs.pdf
(contains corrections of the tables)

Table of odd palindromes of size 1 and 3:

                                        

Table of even palindromes of size 2 and 4:

Notes on the Tabularity of Polycontextural Logics

Bifunctoriality and Tabular Notation for Polycontextural Logics

Some new developments in the formalization of tabular logics as attempts to a non-hierarchical and not-tree-based paradigm of formal thinking.


Western Logic and Trees
Logic is easily connected with trees. Raymond Smullyan started the movement of “Logic with Trees” (Colin Howson), Melvin Fitting, the master of all trees dedicates his book “First-order Logic and Automated Theorem Proving" "To Raymond Smullyan who brought me into the trees".

The tree or tableaux method is highly elaborated by Melvin Fitting as the ultimate tableaux method, used today as a proof method for nearly all kinds of logical systems. There had been predecessors, as usual, like Evert Beth and Jaako Hintikka, or the Dialog Logic approaches of Paul Lorenzen and E. M. Barth.

Tree-thinking goes back to the Porphyry of Tyre with his Porphyrian tree. Tree-thinking is fundamental for Western thinking. Chinese thinking in contrast is based not on trees but on grids (Yang Hui (楊輝, c. 1238 - c. 1298)).


http://the-chinese-challenge.blogspot.co.uk/2007/03/chinese-centralism.html

The tableaux approach to logic seems to be very natural. Its emphasis is focussed on a structure with a singular beginning (root) and (mostly) binary decision procedures for the prolongations of the tree build on the base of such a root and its branching. The established hierarchy between the root and its nodes is perfectly stabilized by the success of its applications and its lucid rationality rooted in classical Western thinking of Porphyrian tree-ontology and its re-invention in the Semantic Web, too.

It is believed, historically and actually, that non-rooted and non-hierarchical systems of thought and action are leading for short or long into chaos.

Postmodernist thinking believes that such arguments of and against hierarchical organizations are obsolete. Even the smallest kid experiences and knows how much we all are connected and taking part in massive networks where there is no beginning and no end and everything is nevertheless working fine. What’s a correct impression for kids is not necessary the truth of the adult game.

With or without clouds, the internet connections are strictly hierarchically mathematized, programmed, organized, regulated, governed and policed.

The mass of data and “contents” are blinding the fact of the covered simple hierarchical form of organization of the deep-structure of the Web. Not just ICANN and the reduction to uni-directional communication but also the reduction of any sign system to techniques and ideologies of digitalism is determining the structural poverty of the overwhelming possibilities on an informational data-level.

Towards Matrix-based Logics

For whatever reasons I never could find any enthusiasm for such an ultimate tree.

To stay in the context of the established form of rationality I prefer to live with/in forests instead of singular trees. I don’t see any reason why a node might not change into a root and a root not becoming a node of a different, equally fundamental tree.

Traditional trees are not just defined by their uniqueness and hierarchy but by the their definitive lack of interchangeability, chiasm or proemiality of the ‘fundamental’ terms, like nodes and root.

In fact, trees don’t come in plural. All the singular and factual trees, say of logic, are dominated by the concept and methods of a single, unique and ultimate idea of a tree.

A first, and simple approach to surpass such limitations is proposed with the idea and some elaborations of forest-based polycontextural logics.

Hence, nothing is wrong with “Logic with Trees”. I opt to just disseminate such ultimate trees. This, as such and alone, wouldn’t be specially interesting. What makes the forest approach interesting is the possibility of interactions between the plurality of such simultaneously existing ultimate trees. A forest is not the sum of singular trees but the interactivity between trees.

Forests of Tableaux-Trees

For the case of just one singular but ultimate tree we don’t have to know much about the structure of the place it is planted. Because of its uniqueness the knowledge of its ground(ing) can freely be omitted. For a forest, the loci of the trees becomes crucial. Disseminated trees are indexed to localize them in the grid of the ground. A ground and locus of a tree is not itself a tree. Hence, any logical characterization of the loci of the trees, that is building of a matrix and a grid, is obsolete. The matrix of the dissemination of logic-trees is defined by a a-logical or pre-logical structure. This pre-logical and pre-semiotic structure is covered by the methods of kenogrammatics. Thus, the grid of the forest is the kenomic matrix.

Again, the game starts again. There is no necessity to suppose a static hierarchy between the grid and the forests.

Trees in formal languages are reduced to the simple structure of “append”  and “remove” of “items”. Hence, disseminated trees are indexed, in this case, double-indexed to define a matrix of trees, and are defined by the similarly simple operations of “leave” a tree, ‘horizontally’ for replications (reflection) and “leave” a tree vertically for transpositions (transjunctions).

Other operations between trees, like permutation, reduction and iteration of trees of a forest, are easily introduced and implemented into the formal game of forest-logics. Forests are not static. They might grow or shrink and change their patterns.

From a more mathematical point of view, forests and their interplays are well ruled by the polycontextural concept of interchangeability, i.e. a generalization and subversion of the category-theoretic concept of bifunctoriality.

Without any big deviations and dangerous revolutions a move from the tree-culture to a forest-world of thinking and acting seems to be a fairly save and sane step of evolution even for the timid Western searcher of truth and computational efficiency.

In earlier papers about tree-farming I proposed contextural forests as forests of colored trees. This time, coloring has to wait for the paint.

Full text:
http://memristors.memristics.com/Notes%20on%20Polycontextural%20Logics/Notes%20on%20Polycontextural%20Logics.html
http://memristors.memristics.com/Notes%20on%20Polycontextural%20Logics/Notes%20on%20Polycontextural%20Logics.pdf

Zu einer Komplementarität in der Graphematik

Semiotik zwischen Browns Unterscheidungen und Mersennes Differenzierungen

FULL TEXT
http://www.thinkartlab.com/Memristics/Komplementaritaet/Komplementarität%20in%20der%20Graphematik.pdf

This German Text explains some points of the paper "Complementary calculi" published at: http://memristors.memristics.com/Complementary%20Calculi/Complementary%20Calculi.html

Abstract

Die Komplementarität zwischen dem Kalkül der Unterscheidung im Sinne Spencer-Browns und dem Mersenne Kalkül der Differenzierung wird in nicht formaler Weise kurz skizziert. Dabei werden auch verschiedene z.T. historische Anmerckungen notiert. Anwendungsbespiele der Komplementarität für ein Verständnis der Objekttheorie im Rahmen einer Semiotik, und Reflexionen zur Selbstreferentialität der Reentry-Form und der Form der Selbst-Zitation werden angedeutet. Es wird zwischen kontextunabhängigen und kontexabhängigen, d.h. morphogrammatischen Kalkülen der Unterscheidung und der Differenzierung differenziert.

Objekte der Semiotik angesichts ihrer Janus-Köpfigkeit

The law of complementarity
"There is no stronger mathematical law than the law of complementarity. A thing is defined by its complement, i.e. by what it is not. And its complement is defined by its uncomplement, i.e. by the thing itself, but this time thought of differently, as having got outside of itself to view itself as an object, i.e.`objectively', and then gone back into itself to see itself as the subject of its object, i.e.`subjectively' again. (George Spencer-Brown, Preface to the fifth English edition of LoF)

Objekte werden in der Semiotik differenziert durch Identifikation und Separation. Die Gesetze der Differenzierung sind nicht die Gesetze der Unterscheidungen wie sie durch das Kommado: "Triff eine Unterscheidung! (Draw a distinction!) markiert werden.

Zeichen in der Semiotik werden durch Unterscheidungen von Innen und Aussen konstitutiert. Das Innen-Aussen-Verhältnis definiert eine Zwei-Seiten-Form. Diese wiederum werden grundsatzlich durch den Kalkül der Unterscheidung markiert. Solche dichotomen Gebilde werden dann als Zeichen verstanden.

Der Aspekt der differenz-theoretischen Eigenschaften von Zeichen wurde von Niklas Luhmann herausgestellt. Selbst wenn seine Charakterisierung primär auf den selbst-referentiellen Charackter der Verweisungszusammenhänge insistiert, ist das Zeichen bei Luhman als eine 2-Seiten-Form bestimmt.

Der Semiotiker Alfred Toth hat in verschiedensten Anläufen das Verhältnis von Zeichen und Objekt thematisiert und versucht einer post-semiotischen Behandlung zugänglich zu machen. Eine starke Verallgemeinerung des Peirce-Bense'schen Zeichenbegriffs ist ihm gelungen durch eine Radikalisierung der Zeichen/Objekt-Beziehung zu einem Innen/Aussen-Verhältnis. 

Beide, Toth wie Luhmann, benutzen als Apparat der Argumententation in wesentlichen Teilen Spencer-Browns Calculus of Indication, beide mit dem Anspruch und Glauben, damit über die Einschränkungen der Logik hinaus gelangen zu können.

Wie ich in einer fruheren Arbeit angefangen habe aufzuzeigen, lässt sich Luhmanns Ansatz vom Second-Order Cybernetics Jargon befreien, ohne dass dabei seine Erkenntnisse aufgeben werden müssten. Es wurde aufgezeigt, dass eine sog. Diamond-Theoretische Thematisierung direkter und prinzipieller den Umstand der Zeichenform als Zwei-Seiten-Form erfasen lässt.

Durch weitere Arbeiten meinerseits, die erst vor kurzem in einer etwas ausführlicheren Form publiziert wurden, scheint es möglich geworden zu sein, auch den objekt-theoretischen Aspekt der Zeichenbildung, unter der Verallgemeinerung von Innen und Aussen, als eine zur Theorie der Unterscheidung komplementäre Form zu bringen. Und zwar durch den neu eingeführten Calculus of Differentiation. Es wurde in aller Ausführlichkeit gezeigt, dass und wie die beiden Sichtweisen der Unterscheidung und der Differenzierung zu einander komplementär sind.

Im allgemeinen wird der Unterschied zwischen einer Dualität und einer Komplementarität in einem Kalkül, bzw. zwischen Kalkülen, nicht klar gesehen. Dualität existieren für nahezu alle denkbaren Kalküle, auch etwa für den Kalkül der Aussagenlogik oder abstrakter, für die Kategorientheorie, und hat dort die Funktion, die in Grossbritanien zu einer verkaufs-technischen Belästigung geworden ist, des "Two for One".

Im Gegensatz dazu sind komplementäre Kalküle oder Kalküle der Komplementarität nicht leicht zugänglich, und fristen ein isoliertes Dasein, etwa in der Quantenlogik.

Wurde die Bedeutung der sog. Quadralektik, d.h. des 4-fachen chiastischen Zusammenspiels von Innen und Aussen betont, und im Grundzug formalisiert, ist jezt ein expliziter Formalismus etabliert worden, der diesen komplementären Aspekt des Aussen-Innen-Verhältnisses formal und operativ zu erfassen vermag.

Wird der Kalkül der Unterscheidung (Calculus of Indication, CI) mit dem Namen George Spencer-Browns, als dessen Schöpfer verbunden, schlage ich vor, den neuen Kalkül der Differenzierung (Calculus of Differentiation, CD) mit dem Namen des Metaphysikers und Mathematikers Marin Mersenne (1588 - 1648) in Verbindung zu bringen, und daher die Bezeichnung Mersenne Kalkül zu wählen.

Sollte es diesen Mersenne Kalkül überhaupt geben, würde allerdings dadruch die Einzig(artig)keit des Brown'schen Kalküls radikal relativiert. Der Calculus of Indication der Laws of Form würde damit nicht nur klar von der Form der Logik unterschieden, bzw. exakt unterscheidbar gemacht, sondern der CI kriegte nun, ganz im Widerspruch zu seinem Anspruch und seiner Intention, ein komplementäres Spiegelbild vorgesetzt. Ein solches Spiegelbild muss nicht symmetrisch sein, sonst wäre es schlicht eine Dualität.

Es stellt sich grundsatzlich heraus, dass beide Kalküle, wie auch der von beiden unterschiedene Logikkalkül, eine Realisierung eines passenden Schriftsystems der allgemeinen Theory der Schreibweisen, d.h. der Graphematik, darstellen, und somit in einen umfassenden systematischen Zusammenhang gestellt werden können, ohne dass dabei die eine oder andere Dogmatik bevorzugt werden müsste.

Wolframs Brownesker Tweet: "More than one is one but one inside one is none.", kriegt von der Mersenne App automatisch einen Retour-Tweet: "More than one is none but one inside one is one."

FULL TEXT
http://www.thinkartlab.com/Memristics/Komplementaritaet/Komplementarität%20in%20der%20Graphematik.pdf

Complementary Calculi: Distinction and Differentiation

George Spencer-Brown and Marin Mersenne

Headaches with complementary calculi

If two formal systems have a very close familiarity as a duality or even a complementarity, and are therefore to some degree nearly indistinguishable, but you nevertheless discovered in a strange situation of an insight a decisive difference between them. 

Then it might easily be possible, as in my case, that you get nightmares of endless oscillations and manifestations of something you don’t yet have access to, and what, as far as you guess, what it could be, you anyway wouldn’t like at all.

That’s what happens with the discovery of the complementary calculus of indication, a calculus I call a Mersenne calculus of differentiation and separation, in contrast to the Spencer-Brown calculus of indication and distinction. 

I have never been a friend of this calculus of The Laws of Form, therefore to get involved with its complementary calculus is no pleasure at all.

Obviously, to get rid of the headache with the CI and its ambitious and annoying celebrations, especially in German humanities, the best is to show, or even to prove, that there is a complementary calculus to the calculus of indication, too.

With that, the sectarian propaganda of the CI boils down to a strictly one-sided and utterly blind endeavour.

In-between I have written some papers dealing with the complementarity and applications of the concepts of the CI and the MC.

There might still be too much non-deliberated obfuscation involved, at least, some clear aspects of the new calculus of differentiation, CD, and its complementarity to the calculus of indication and distinction are now elaborated as far as it takes to get a primary understanding of the new situation.

Indication and differentiation in graphematics

Moshe Klein has given a simple introduction to George Spencer-Brown's calculus of indication (CI) as a special case of a bracket grammar. 

A context-free language with the grammar:
                                              S ⟶ SS|(S)| λ
is generating the proper paranthesis for formal languages. 



What was an act of a genius becomes an adhoc decision to restrict the grammar of bracket production.

Set the restriction of bracket rules to:
                                              (()) () = () (())
and you get the basic foundation of the famous CI as introduced by George Spencer-Brown. 

Nobody insists that this is an appropriate approach but it seems that it takes its legitimacy from the formal correctness of the approach.

Now, with the same decisionism, albeit not pre-thought by a genius, I opt for an alternative restriction,
                                             (( )) = ( ).
This decision is delivering the base system for a Mersenne calculus, interpreted as a calculus of differentiation, CD. 



I stipulate that both calculi, the CI and the CD, are complementary. And both calculi have additionally their own internal duality, delivering the dual calculi, i.e. the dual-CI and the dual-CD.

It will shown that, despite of its non-motivated adhocism, both calculi are well founded in graphematical systems, and are to be seen as interpretations of independent complementary graphematical calculi.

In fact, they belong, with the identity system for semiotics to the only two non-kenogrammatic graphematical systems of the general architectonics of graphematics. 

Abstract
The paper "Diamond Calculus of Formation of Forms. A calculus of dynamic complexions of distinctions as an interplay of worlds and distinctions” was mainly based on a deconstruction of the conditions of the calculus of indiction, i.e. the assumption of a “world” and “distinctions” in it. 

The present paper “Complementary Calculi: Distinction and Differentiation” opts for a graphematic turn in the understanding of calculi in general. This turn is exemplified with the George Spencer-Brown’s Calculus of Indication and the still to be discovered complementary Mersenne calculus of differentiations. 


First steps toward a graphematics had been presented with “Interplay of Elementary Graphematic Calculi. Graphematic Fourfoldness of semiotics, Indication, Differentiation and Kenogrammatics".

Graphematic calculi are not primarily related to a world or many worlds, like the CI and its diamondization. Graphematic calculi are studying the rules of the graphematic economy of kenomic inscriptions.


Graphematics was invented in the early 1970s as an interpretation of Gotthard Gunther’s keno- and morphogrammatics, inspired by Jaques Derrida’s grammatology and graphematics. 

Spencer-Brown’s calculus of indication has been extensively used to interpret human behavior in general (Niklas Luhmann). 

The proposed new complementary calculus to the indicational calculus, the Mersenne calculus, might not be applicable to human beings, but there is a great chance that it will be a success for the interaction and study of non-human beings, e.g. robots, aliens, and Others.

FULL TEXT

http://memristors.memristics.com/Complementary%20Calculi/Complementary%20Calculi.html

NEW APPROACHES

NEW APPROACHES TO THE PROJECT OF UNDERSTANDING THE SPECIFIC RATIONALITY OF THE CHINESE WRITING SYSTEM

It is believed that with the understanding of morphograms as rules for morphic cellular automata a new approach for an understanding of the specific rationality of Chinese writing systems is achieved. With that the Blog "THE CHINESE CHALLENGE" enters into a new level of understanding Chinese rationality in a non-Western way.

(For technical reasons I publish these comments on the Blog "Rudy's Diamond Strategies" too.)

This will be elaborated in a special paper.

Here are some papers mentioned that had been on the way to this new understanding of the dynamics and pragmatics of Chinese characters.

An intermediary paper to this understanding was published as "What Chinese Grammar".

What Chinese Grammar?
Interchangeability and morphogrammatics of interpretations 

To put it bluntly: Ancient Chinese characters (signs, hieroglyphs, characters) are
conceived in a transclassic setting as morphograms. 

This insight is achieved with the approach of a polcontextural transformation of the categorical concept of bifunctoriality and understood as the interchangeability of locus of a character and the character itself.
 

Furthermore the interchangeability of Western grammatical categories to characterize Chinese characters and sentences is applied.

This is proposed with the help of a positive reading of Rolf Elberfeld studies (2003, 2007) and a negative differentiation to other approaches which are not reflecting their complicity with Western grammar.

http://www.thinkartlab.com/pkl/media/Chinese%20Grammar/What%20Chinese%20Grammar.pdf

 http://www.thinkartlab.com/pkl/media/Chinese%20Grammar/What%20Chinese%20Grammar.html

The Amazing Power of Four

Gotthard Gunther’s space-travel algorithm and Leon Chua’s Fourth electronic Element supported by Robert Rosen’s speculations about anticipative systems

Speculations about trans-functorial and morphic metamorphosis of space - time and worlds on one side, and flux and charge of electronics on the other side, leading to the memristor and memristive systems of nanoelectronics.

Achievements and attempts to surpass classical paradigms of science by Gotthard Gunther and Leon O. Chua are portrayed and other attempts of Robert Rosen’s anticipatory systems are sketched and Martin Heidegger’s late philosophy of the Fourfold are mentioned. 

http://www.thinkartlab.com/Memristics/Power%20of%20Four/Power%20of%20Four.html

http://www.thinkartlab.com/Memristics/Power%20of%20Four/Power%20of%20Four.PDF

Short Overview of Morphic Cellular Automata

http://memristors.memristics.com/CA-Overview/Short%20Overview%20of%20Cellular%20Automata.html

http://memristors.memristics.com/CA-Overview/Short%20Overview%20of%20Cellular%20Automata.html

Graphematic System of Cellular Automata

Short characterization of cellular automata by the 9 graphematic levels of inscription

As a further specification of the “overview of morphic cellular automata”, described before, a graphematic classification of the inscriptional systems shall be introduced and applied to different types of cellular automata. 

http://memristors.memristics.com/Graphematics/Graphematics%20of%20Cellular%20Automata.html

http://memristors.memristics.com/Graphematics/Graphematics%20of%20Cellular%20Automata.PDF

Towards Abstract Memristic Machines

A new paper about the
 http://memristors.memristics.com/Machines/Memristic%20Machines.html
http://memristors.memristics.com/Machines/Memristic%20Machines.pdf




Abstract
Memristic machines are time-tensed machines of the nanosphere. Their definition and their rules are not covered by ordinary logic, arithmetics and semiotics, basic for a theory of abstract automata. The difference to classical concepts of machines to tensed, i.e. memristive machines is elaborated. As an attempt to develop memristive machines, basic constructs from morphogrammatics are applied.  
Properties of retro-gradeness (antidromicity), self-referentiality, simultaneity and locality (positionality) of operations as they occur in kenogramamtic and morphogrammatic basic operations, like the successor operations, ‘addition’ and ‘multiplication’ have to be realized on all levels of operativity in memristive systems.  
Hence, the tiny memristive properties of time- and history-dependence for kenomic successors are presented for all further operations, like “addition" (coalition), "multiplication”, “reflection”, etc. Morphogrammatics will be further developed in Part II of the paper.


A new framework for design and analysis for memristive systems, i.e. memristics, shall be sketched as a complex methodology of Morphogrammatics, Diamond Category Theory, Diagrammatics and Nanotechnology.

Graphematics of Conflicts

Since my studies of memristics in the framework of trans-classical logic, I developed a new concept of cellular automata, and discovered an interesting application of morphogrammatic-based cellular automata for an interpretation of the pragmatical aspects of Chinese characters.

With this post, I would like to introduce an application of novel distinctions to a theory of conflict management. And an application to a theory of propaganda analysis is proposed.

"Inconsistency robustness is information system performance in the face of continually pervasive inconsistencies–- a shift from the previously dominant paradigms of inconsistency denial and inconsistency elimination attempting to sweep them under the rug.” (Carl Hewitt)
http://carlhewitt.info/

The role of contradictions and gaps in the analysis of propaganda and databases

Some preliminary thoughts and notes about conflict-theory and the strategies of propaganda in politics and science are developed in the framework of graphematics.

This is not yet taking into account the complementary diamond aspects of conflicts.

Orwell’s characterization of propaganda: Newspeak, Doublethink and Memory-loss as a defence of truth are modeled by the features of graphematic calculi as new operative tools of propaganda analysis and deconstruction.

Traditionally, a theory of propaganda is covered by the techniques of rhetorics of speech-acts. Graphematics proposes elements of a deconstruction of propaganda beyond the level of rhetorics.

On one side we have the propaganda analysis of George Orwell based on a defence of truth, on the other side the self-reflections of the propagandist Joseph Goebbels about the rationality of propaganda as being neutral to the categories of truth and false. 


An application of graphematic distinctions to the definition of conflicts in databases is taken as a contrast to explain and demonstrate the functioning of graphematic approaches to conflicts and contradictions, like Boolean, Mersennian, Brownian and Stirlingian.

 LINKS
 http://memristors.memristics.com/Graphematics%20of%20Conflicts/Graphematics%20of%20Conflicts.html

http://memristors.memristics.com/Graphematics%20of%20Conflicts/Graphematics%20of%20Conflicts.pdf